抢红包！为何有些人盆钵满盈，有些人入不敷出？

　　随着春节的脚步临近，无论是某宝、某信还是企鹅，一波一波的红包浪潮已经汹涌袭来，不知道您今年的红包收支是否平衡呢？很多时候我们感慨的不只是手速，还有运气，那为什么有的人挣得钵满盆盈，有的人抢个红包还要赔上流量钱呢？

　　由于微信的红包是一个个抢的，所以很容易给人以这样的印象：红包一堆钱摆在那里，第一个人闭眼抓一把，第二个人再抓一把，等等。但是倘若果真如此，后来的人总体而言就要吃亏。这样既不公平，也不满足现实中的观察。

　　所以，更合理的做法是，一开始就把所有的钱一次性分成几个包，每人抓一个，每个包都是等同的，里面的钱数期望都是总金额的几分之一。满足这个要求的做法当然不止一个，但我们先考虑最符合直觉的办法——切面条。

　　假如你有一根面条要随机分成5根，怎么分？闭上眼睛剁4刀就行了。换成数学语言，就是在一条线段上随机扔4个点，分成5段。

　　现在你要把红包分成5份，好办，拿出你刚才剁的面条，每一根面条有多长，对应的红包就塞多少钱。

　　（当然，面条是连续的，而红包是离散的——每个包的钱数都是1分钱的整数倍。但钱多的时候这点差异无关紧要，而要是有人发了个全一分钱的红包，还是暂停讨论把他踢出群比较好。）

　　以下就是切面条法分红包的一个实例，总金额为1元，分成5个：

　　0.02669467， 0.248426309，0.23745777，0.35864430，0.12877695

　　这贫富差距也太大了吧？如果红包总金额是100，那么领得最多的人可以得到35.86元，而最少的只有2.67元。第一名得到三分之一多的钱，最后一名不到三十分之一？其实这完全不极端。对于这种分法，我们可以数学上证明，当1块钱（或者长度为1的面条）分成n份儿的时候，

　　第k大的值，期望为1/n*(1/n+1/(n-1)+1/(n-2)+…+1/k)。（证明留作练习（被踢飞））

　　所以，最大值的期望为 1/n*(1/n+1/(n-1)+1/(n-2)+…+1)，

　　而最小值的期望为 1/n^2。

　　换言之，在n=5的时候，平均而言，五个人应该分别拿到的红包大小是：0.456666……，0.256666……，0.156666……，0.09，0.04。真是朱门酒肉臭路有冻死骨啊。

　　好吧，虽然这恐怕和很多人的印象相符，但毕竟也太悬殊了，能不能增加一个调节杆，让红包间的差异稍微小一点呢？

　　进阶模型——狄利克雷分布

　　复习一下刚才的切面条模型要点。

　　1 一次可以生成n个随机数，且总和为1，这样每个数乘以红包总金额就是每个人分得的钱；

　　2 每个随机数的期望应该均等，即n分之一，这是为了保证大家抢红包机会平等；

　　现在我们为它增加一个第三条：

　　3 有一个参数可以用来调节红包的“公平”程度。这里的公平不是指机会公平，而是说每次发红包大家实际拿到手的钱是不是相近，即金额分配的波动性是大还是小。比如100元的红包发给10个人，如果每人都是10元左右，我们认为这种分配更公平些；如果最少的才0.8元，最多的有20元，显然就有失公允了（不幸的是作者好几次碰到这种情况……）。

　　幸运的是，在众多的随机变量分布中，有一个“狄利克雷分布”非常适合上面列出的这些情况。狄利克雷分布本身有n个参数，但为了满足条件2，我们可以只用一个参数 α 来决定它的具体形式。α 越大，每人分得的金额比例就越倾向于平均，反之则波动性越大。

　　更幸运的是，我们开始提出的切面条分法，恰恰就是当α=1的时候，狄利克雷分布的最简单状态。

　　刚才切面条的结果，也就是α=1时的狄利克雷分布生成的随机数

　　0.02669467， 0.248426309，0.23745777，0.35864430，0.12877695

　　而下面是α=10时的一组随机数

　　0.2459250，0.2722147，0.1717301，0.1398133，0.1703169

　　可以看出，当α=1时，金额分配的变动性非常大，而在α=10的情形下，金额的分配就平均多了。

　　红包越公平，财富差越大

　　前面提到，在我们的模型中有一个参数 α 用来控制红包金额分配的“公平”程度（或者更准确地说，是“平均”的程度，因为就机会而言，每个人分得金额的可能性都是相同的，但就每一次实际分得的金额而言，α 越大，这种分配越倾向于平均，即结果的波动性越小）。下图展示了一组随机模拟实验的结果，其中我们模拟了20次红包接力的游戏，10次取 α=2， 另外10次取 α=20。每次游戏中，红包都接力了500次。

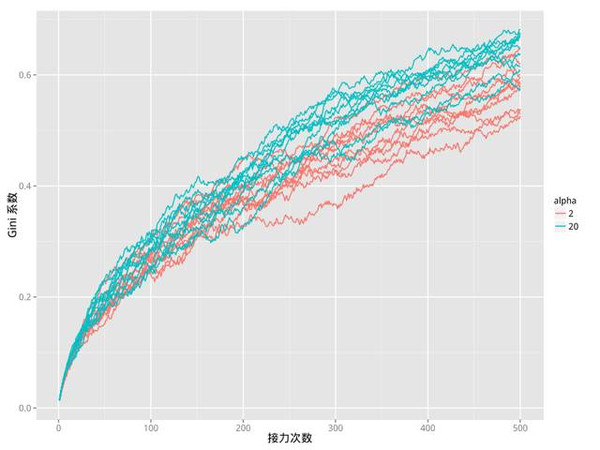
　　可以看出，红线和蓝线虽然有所重叠，但总体来看蓝线的取值要比红线更大，也就是说，红包金额越“公平”，贫富差距反而会越大。

　　这个结论看起来可能有些反直觉，但其实也合情合理：如果红包的分配是绝对公平的，那么第一名得到的金额就将是2元，而下一轮又必须送出20元，所以 总共亏损18元；如果红包金额的波动性很大，就会有一部分人得到的金额小于2元，而第一名就会得到更多，也就更不容易破产。所以说，一个规则是否真的“公平”，不能只看其表面。

　　来源：果壳

《抢红包！为何有些人盆钵满盈，有些人入不敷出？》由河南新闻网-豫都网提供，转载请注明出处：http://edu.yuduxx.com/sxks/zk/399865.html，谢谢合作！