乐多多：小学数学应用题公式大全（二）

　　著名儿童文学作家 乐多多/总结推荐

　　选自 乐多多主编的图书《小学生一看就懂一学就会的数学窍门书》

　　每个孩子做应用题必用公式，可是公式忘记了怎么办？

　　备一份应用题公式大全。

　　哦，这只是一个权宜之计，这次查公式，孩子做对了题，下次还查公式……那下下次，或者考试时怎么办？

　　所以，教孩子记住公式是如何推导出来的，帮他（她）彻底把公式理解，这就相当于帮他（她）把公式刻在了脑子里，这下想忘都忘不了了。

　　想家长所想，急家长所急，乐多多早就已把小学必用的公式，及推导过程备齐喽。

　　5．行船问题公式

　　（顺水速度＋逆水速度）÷2＝船速

　　（顺水速度－逆水速度）÷2＝水速

　　顺水速＝船速×2－逆水速＝逆水速＋水速×2

　　逆水速＝船速×2－顺水速＝顺水速－水速×2

　　【例题】一艘船顺水行320千米需要8小时，风平浪静时船速为每小时25千米，问，这只船逆水行这段路成需要多少小时？

　　【公式推导过程】顺水情况下的船速（顺水速度），逆水情况下的船速（逆水速度）和风平浪静时的船速（船速）是不一样的概念，因为顺水行船的时候，水速是推动船前进的动力，因此，顺水划船比较省力。这时，顺水速度就等于静水船速加上水的速度。而逆水行船时，水速是阻碍前进的阻力，因此，逆水滑船比较费力。这时，逆水速度就等于静水船速减去水流的速度。

　　据此，我们可以得出解决这类题基本的运算公式：

　　顺水速度＝静水船速＋水速

　　逆水速度＝静水船速－水速

　　结合这两个基本公式，我们还可以推导出以下几个公式：

　　静水船速＝（顺水速度＋逆水速度）÷2

　　水速＝（顺水速度－逆水速度）÷2

　　顺水速度＝静水船速×2－逆水速度＝逆水速度＋水速×2

　　逆水速度＝静水船速×2－顺水速度＝顺水速度－水速×2

　　【例题解题步骤】

　　解：顺水速度为：320÷8＝40（千米/小时）

　　水速为：40－25＝15（千米/小时）

　　逆水速度为：25－15＝10（千米/小时）

　　逆水时间为：320÷10＝32（小时）

　　答：这只船逆水行驶这段路程需要32个小时。

　　6．列车问题公式

　　火车过桥：过桥时间＝（车长＋桥长）÷车速

　　火车追及： 追及时间＝（甲车长＋乙车长＋距离）÷（甲车速－乙车速）

　　火车相遇： 相遇时间＝（甲车长＋乙车长＋距离）÷（甲车速＋乙车速）

　　【例题】一座大桥长3000米，一列火车以每分钟800米的速度通过大桥，从车头开上桥到车尾离开桥总共用了4分钟。问，这列火车长多少米？

　　【公式推导过程】当火车头上桥的时候，火车尾还在桥的外面；当火车头走下桥时，火车尾还在桥上，即还没有过完桥，因此火车还要继续向前行走，直到火车尾离开桥时，才算过完了桥。所以，火车过桥的过程即为：从火车头上桥到火车尾离开桥。

　　而当火车尾离开桥时，事实上火车头多走了一个火车车身长度的距离，所以说，火车过桥实际所走的路程就等于桥的长度加上火车车身的长度。用公式表示就是：火车过桥实际所走的路程＝桥的长度＋火车的长度。

　　分析这个计算过程，我们还可以将火车过桥的公式总结为：

　　过桥时间＝（桥长＋车长）÷车速

　　车速＝（桥长＋车长）÷过桥时间

　　【例题解题步骤】

　　解：800×4＝3200（米）

　　3200－3000＝200（米）

　　答：火车的长度为200米。

　　7.植树问题公式

　　线形植树 棵数＝距离÷棵距＋1

　　环形植树 棵数＝距离÷棵距

　　方形植树 棵数＝距离÷棵距－4

　　三角形植树 棵数＝距离÷棵距－3

　　【例题】在一条长48米的路的一侧植树，两端都要植树，如果平均每隔2米植一棵树，那么，一共要植多少棵树？

　　【公式推导过程】在讲植树问题的时候，老师经常提到“封闭性路线”和“非封闭性路线”， 这里一定要注意，非封闭性路线植树问题还可以分为三类：一类是两端都植树的情况；一类是两端都不植树的情况；还有一类是一端植树一端不植树的情况。具体情况不同，所植的树的数目也会不同，所以，这需要我们做题时一定要仔细分析和辨别，先确定植树的路线属于哪种情况。

　　我们都知道，上述的题目是一道典型的非封闭路线两端都植树的问题。

　　正确的解题方法应该是怎么样呢？在讲解这道题之前，我们先来试想一下，把一个线段平均分成三份，两端都有端点是什么样的呢？一共有几个端点呢？

　　我们可以在纸上画一个线段图，如下：

　　从这个线段图可知，一条线段被平均分成了三个部分，一共有四个点。

　　按照上面的分法再试着画一下，把一个线段平均分成四份，你会发现，线段上有5个点；把一个线段平均分成5分，线段上有6个点……

　　综上所述，我们发现，把线段平均分成几份，要求首尾两端都有点，那么点数总是比间隔数多1。

　　非封闭路线上，两端都植树也是同样的道理。因此，我们可以总结出解决非封闭路线上，两端都植树的问题一般公式：

　　棵数＝间隔数＋1；

　　间隔数＝总距离÷间隔长；

　　所以，棵数＝总距离÷间隔数＋1；

　　弄清楚了这一点，上面那道题就很容易解决了。

　　间隔数＝总距离÷间隔长＝48÷2＝24（个）。

　　棵数比间隔数多1。

　　所以，植树的棵树为：24＋1＝25（棵）

　　【例题解题步骤】

　　解：48÷2＝24（个）

　　24＋1＝25（棵）

　　答：植树的棵树为25棵。

　　8．鸡兔同笼问题公式

　　第一鸡兔同笼问题：

　　假设全都是鸡，则有

　　兔数＝（实际脚数－2×鸡兔总数）÷（4－2）

　　假设全都是兔，则有

　　鸡数＝（4×鸡兔总数－实际脚数）÷（4－2）

　　第二鸡兔同笼问题：

　　假设全都是鸡，则有

　　兔数＝（2×鸡兔总数－鸡与兔脚之差）÷（4＋2）

　　假设全都是兔，则有

　　鸡数＝（4×鸡兔总数＋鸡与兔脚之差）÷（4＋2）

　　【例题】一个笼子里养着兔子和鸡，总共有50只，而它们的脚总共有160只，那么鸡、兔子各有多少只？

　　【公式推导过程】首先，根据条件，鸡兔共有50只，脚共有160只。那么，假设50只全是鸡。

　　其次，根据假设进行分析，一只鸡有2只脚，如果有50只鸡，那么共有脚2×50=100只。

　　但是题目中告诉我们，共有脚160只，假设的情况比实际情况少了

　　160－100=60只脚。

　　最后，分析原因。因为每只兔子有4只脚，即一只兔子比一只鸡多2只脚，在假设情况中，把兔子当成了鸡，即是，每只兔子少算了2只脚，总共少算了60只脚。

　　因此兔子的只数是：60÷2=30（只）。

　　那么，鸡的只数是：50－30=20（只）。

　　小朋友，根据上面那道题，你能不能总结出解决鸡兔同笼问题的关系式呢？

　　通过很多鸡兔同笼问题，假设全部都是鸡的话，有这样的关系式可以直接代入：

　　兔子数=（总脚数－2×总数）÷（4－2）；

　　注意：2是一只鸡的脚数，4是一只兔子的脚数。

　　假设笼子里都是兔子，那么有这样的关系式可以直接代入：

　　鸡数=（4×总数—总脚数）÷（4—2）；

　　注意：2是一只鸡的脚数，4是一只兔子的脚数。

　　【例题解题步骤】

　　解：兔子的只数是：60÷2=30（只）。

　　鸡的只数是：50－30=20（只）

　　答：有兔子30只，鸡20只。

　　9.追击问题公式

　　追及时间＝追及路程÷（快速－慢速）

　　追及路程＝（快速－慢速）×追及时间

　　【例题】一匹千里马一天能跑150千米，一匹普通的马一天能跑90千米。普通马先跑12天，千里马几天能追上它？

　　【公式推导过程】这道题让我们求千里马追上普通马的时间，我们都知道路程问题的关系式是：时间＝路程÷速度，那追击问题的关系式是怎样的呢？

　　别急，我们一起画图来推导：

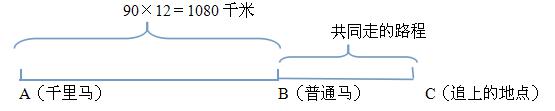
　　A（千里马） B（普通马） C（追上的地点）

　　（1）从上图中可以看出，线段BC之间的距离为追击时间内两马共同走的路，所以，普通马提前走的那段距离即为追击路程，即线段AB之间的距离（此处大家一定要记住，追击时间内，速度快的比速度慢的多走出的距离，就是追击路程）。而追击时间为千里马跑完全程的时间，或者普通马跑完线段BC的时间。

　　（2）当千里马追上普通马的时候，普通马跑的路程是：90×12＋90×追及时间。90×12是追及路程。因为普通马跑得慢，我们就称它为慢速，上面的算式可以改写为：追及路程＋慢速×追及时间。

　　（3）因为千里马跑得快，我们就称它为快速，那么千里马跑的路程就是：快速×追及时间。

　　（4）因为千里马追上了普通马，所以他们跑的路程是一样的，即：追及路程＋慢速×追及时间＝快速×追及时间。

　　（5）对上述公式进行变形，就可以得到：追及路程＝快速×追及时间－慢速×追及时间，再进一步化简变形就得到：追及路程＝（快速－慢速）×追及时间。

　　（6）进一步变式即可得到：追及时间＝追及路程÷（快速－慢速）。

　　这两个公式可是解决追及问题的金钥匙，大家一定要牢牢记住。如果题目比较简单，可以直接运用公式；如果题目比较复杂，还需要我们找出对应的条件转换一下，再利用公式计算。

　　【例题解题步骤】

　　解：90×12＝1080（千米）

　　1080÷（150－90）＝18（天）

　　答：千里马18天才能追上普通马。

　　【更多文章，请关注微信公众号-乐多多儿童文学作家lddbook】

　　孩子与您将获得免费的、长期的、与众不同的成长指导与建议！

　　附：乐多多简介

　　乐多多，著名儿童文学作家，1000 0000畅销童书“胡小闹日记”系列图书作者。已出版30余册、近200万字的儿童文学作品，其作品多以校园成长的某些关键问题为主题，关心小朋友的校园生活和心灵成长，被众多媒体誉为“新时期少年儿童的心灵之作”。“胡小闹日记”系列风靡全国，很多小朋友都从“胡小闹”身上获益良多。

《乐多多：小学数学应用题公式大全（二）》由河南新闻网-豫都网提供，转载请注明出处：http://edu.yuduxx.com/sxks/zk/282933.html，谢谢合作！